GRUNDLAGEN von 3 D TECHNOLOGIEN /// Java3D API /// Autorenwerkzeuge zur Gestaltung
 
 

GRUNDLAGEN:

Zur Berechnung eines 3D Universums sind im wesentlichen vier Schritte entscheident: Koordinatensysteme,Transformation,Projektion und der Betrachter.

1. Drei Koordinatensysteme

Die wichtigste Grundlage für 3D Applikationen bildet das kartesiche Koordinatensystem mit drei Dimensionen x, y und z. Die Beschreibung und Berechnung unseres dreidimensionalen Cyberspace findet zunächst nur im Speicher des Computers statt, ohne dass eine visuelle Ausgabe erfolgt. Jedes Objekt innerhalb dieser Welt muss nun drei verschiedene Koordinatensysteme verwenden:
 

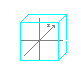	1. Lokale Koordinaten
	Die lokalen Koordinaten definieren ein lokales Koordinatensystem für jedes 3D Objekt unseres Universums. Jedes 3D Objekt hat seinen eigenen Ursprung (0,0,0). In Bezug zu diesem Urspung werden alle Scheitelpunkte des Objektes definiert.
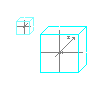	2. Welt Koordinaten
	Die Welt Koordinaten beschreiben das Koordinatensystem des gesamten virtuellen Universums. Alle 3D Objekte innerhalb dieses Universums werden mit ihrem lokalen Ursprung an den Punkt verschoben, an dem sie sich befinden sollen.
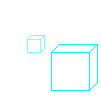	3. Bildschirm Koordinaten
	Nachdem nun alle Objekte an ihren Platz in unserem virtuellen Universum verschoben sind, müssen sie am Bildschirm dargestellt werden können. Dabei ergibt sich aber die Schwierigkeit, dass nun die dritte Koordinate wegfällt. Dabei müssen dann die x und y Koordinate entsprechend umgerechnet werden. Diesen Vorgang nennt man Projektion von 3D auf 2D und er wird im nächsten Absatz beschrieben.

Nachdem wir nun die drei Koordinatensysteme kennengelernt haben, werden wir eine JAVA Klasse für einen Scheitelpunkt entwerfen. Dieser Punkt wird zwei Koordinatentripel und ein Koordinatentupel enthalten, für die beiden Koordinatensystem (lokal, Welt) je drei Werte x,y, und z, für das Koordinatensystem des Bidlschirms nur x und y. Der konstruktor für so ein Punkt Objekt speichert die übergebenen double Werte als die lokalen Koordinaten des Punktes ab.

public class Point3D {

   double lx, ly, lz; // lokale Koordinaten
   double wx, wy, wz; // Weltkoordinaten
   double sx, sy; // Bildschirmkoordinaten

   public Point3D(double X, double Y, double Z) {
      this.lx = X;
      this.ly = Y;
      this.lz = Z;
      }
   } // class

Nun haben wir ein JAVA Objekt zur Verfügung, um die Scheitelpunkte eines 3D Objektes zu beschreiben. Jetzt fehlt uns noch eine JAVA Klasse für ein 3D Objekt. Der Einfacheit halber wählen wir hier ein Rechteck, aber es ist ohne weiteres möglich, komplexere Objekte wie zum Beispiel Würfel oder komplexeres zu konstruieren.

import java.awt.*;     // wegen Color

public class Rectangle3D {

   protected Point3D p1, p2, p3, p4; // Die vier Eckpunte
   protected boolean visible = true; // Für BackfaceCulling
   protected Color color;            // Farbe der Fläche

   public Rectangle3D(Point3D P1, Point3D P2, Point3D P3, Point3D P4)
      {
      this.p1 = P1;
      this.p2 = P2;
      this.p3 = P3;
      this.p4 = P4;
      }
   } // class

Diese Klasse verwendet bereits den oben entworfenen Point3D, um die vier Eckpunkte des Rechecks zu speichern. Die Variablen color und visible werden hier noch nicht benötigt.

2. Visionen der Projektion

Gehen wir nun davon aus, dass unser virtuelles Universum bereits im Speicher des Computers existiert. Das allein wäre ziemlich langweilig, also brauchen wir eine Methode, unseren Cyberspace auch visuell darzustellen. Da unsere heutige Hologrammtechnik noch nicht so weit fortgeschritten ist, müssen wir uns mit dem zweidimensionalen Bildschirm zufrieden geben. Aber unser Universum ist doch dreidimensional? Wir müssen nun eine Möglichkeit finden, unsere Objekte auf den 2D Bildschirm zu projizieren. Die gängigste Möglichkeit zur realistischen Darstellung ist die perspektivische Projektion. Dabei wird die z Koordinate durch Umrechnungen in die x und y Koordinate eingegliedert. Bei der Beobachtung der realen Welt stellt sich schnell heraus, dass weiter entfernte Objekte kleiner erscheinen als die näheren Objekte. Folgende Formeln könnten das ausdrücken:

X_Bildschrim = X_Welt / Z_Welt
Y_Bildschirm = Y_Welt / Z_Welt

Wir teilen einfach die x und die y Weltkoordinaten für die Darstellung auf dem Bildschirm durch die z Weltkoordinate, um der Tiefe des Raumes gerecht zu werden. Es stellt sich jedoch heraus, dass dieser Effekt die Objekte zu stark verkleinert. Bereits in geringer Entfernung schmelzen die Objekte zu kleinen Punkten zusammen. Also erweitern wir die Formel indem wir mit einem Faktor Betrachter_Entfernung multiplizieren. Ebenso wird es problematisch, wenn die z Weltkoordinate gegen 0 geht. Dann wachsen die x und y Bildschirmkoordinaten gegen unendlich und um das zu verhindern addieren wir noch einen Korrekturfaktor korrekt in der Formel hinzu.

X_Bildschrim = Betrachter_Entfernung * X_Welt / (korrekt + Z_Welt)
Y_Bildschirm = Betrachter_Entfernung * Y_Welt / (korrekt + Z_Welt)
 

Der Faktor Betrachter_Entfernung legt fest, wie weit der Betrachter des Universums von der Projektionsfläche (also dem Bildschirm) entfernt ist. Daraus ergibt sich auch der Blickwinkel des Betrachters wie nebenstehende Grafik verdeutlicht. Wenn die Entfernung des Betrachters genau der Hälfte der Projektionsflächenbreite entspricht, dann ist der Blickwinkel 90 Grad. Bewegt sich der Betrachter näher an die Fläche so wird der Winkel grösser. Da Menschen für gewöhnlich einen Blickwinkel von bis zu 150 Grad haben sollte die Entfernung etwas kleiner als die Hälfte der Projektionsflächenbreite gewählt werden.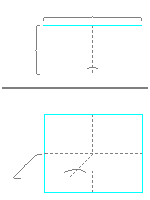

Zur Auflockerung der Materie nun wieder etwas Quellcode, nämlich unsere Methode für die Projektion:

public void project3DTo2D(Rectangle3D r) {
   int distance = 40;
   int xoffset = Screen.width/2;
   int yoffset = Screen.height/2;

   Point3D p[] = { r.p1, r.p2, r.p3, r.p4 };

   for (int i=0; i<4; i++) {
      p[i].sx = 200 * p[i].wx / (p[i].wz+distance) + xoffset;
      p[i].sy = 200 * p[i].wy / (p[i].wz+distance) + yoffset;
      }
   } // project3DTo2D

Die Methode übernimmt ein Objekt unserer Rectangle3D Klasse und speichert dessen 4 Eckpunkte unseres Point3D Typs in einem Array ab. Dies soll nur den Code etwas verkürzen. Wir könnten genausogut eine Projektions-Methode schreiben, die nur einen einzelnen Punkt übernimmt, dann müssten wir auf die Eckpunkte unseres Rechtecks an anderer Stelle im Programm zugreifen und sie an diese Methode schicken. So können wir der Methode bequem ein ganzes Rechteck schicken.
Das Array wird dann in einer Schleife durchlaufen und nach obigen Formeln werden die Weltkoordinaten in Bildschirmkoordinaten umgerechnet. Interessant hierbei noch xoffset und yoffset. Da das JAVA Koordinatensystem den Nullpunkt in der oberen linken Ecke setzt, verschieben wir alle Bildschirmkoordinaten noch um diese offsets, damit das Objekt auf der Bildschirmmitte plaziert wird.

Projection done. Nun da wir wissen, wie wir unsere 3D Objekte positionieren und projizieren können, wenden wir uns nun der Transformation zu.

3. Magische Transformation

Kommen wir nun also zu dem vorerst komplexesten Part der 3D Programmierung: Den Transformationen. Dabei gibt es drei verschiedene Arten von Transformationen: Verschiebung, Skalierung und Rotation. Letztere ist mit Abstand die komplexeste und wohl auch diejenige Transformation, die während eines Programms am meisten ausgeführt wird.

Zur weiteren Vereinfachung der Berechnungen aller Transformationen wird die Matrizenrechnung verwendet. Mit ihr ist es möglich, alle Transformationsprozesse durch Matrizen auszuführen und diese Matrizen zu einer einzigen Transformationsmatrix zusammenzufassen. Mit dieser werden dann einfach alle Scheitelpunkte der zu Transformierenden Objekte multipliziert. Nun ist es an der Zeit, mit etwas Mathematik zu beginnen. Dreidimensionale Punkte werden wir nun wie folgt darstellen: [ xw, yw, zw, w ]. Dabei stellen x, y und z die Koordinaten in unserem Cyberspace dar und das w ist ein sogenannter normalisierender Faktor. Dieser ist nur von mathematischer Bedeutung für die folgenden Berechnungen und soll uns nicht weiter stören. Um die Koordinaten des Originalpunktes zu erhalten, teilen wir einfach alle Koordinaten des Punktes durch w und erhalten: [ x, y, z, 1 ].

Verschiebung

Kommen wir nun zu unserer ersten Transformation. Diese verschiebt ein Objekt um eine Verschiebungs_Faktor. Dies kann zum Beispiel die Geschwindigkeit eines 3D Objektes sein:

X_Neu = Verschiebungs_Faktor + X_Alt
Y_Neu = Verschiebungs_Faktor + Y_Alt
Z_Neu = Verschiebungs_Faktor + Z_Alt

Übertragen wir das nun in die Matrizenrechnung, die uns ja später die Transformationen erleichtern soll. Wir brauchen also eine Matrix die multipliziert mit dem Vektor [ x, y, z, 1 ]das Ergebnis:
[ (x + tx), (y + ty), (z + tz), 1 ] liefert. Dabei gehen wir sogar etwas weiter als in den obigen Formeln und verwenden für jede Koordinate einen anderen Verschiebungsfaktor. Die Matrix, die uns dieses Ergebnis liefert hat folgende Form:

Skalierung

Diese Operation ist noch sehr einfach. Um ein Objekt zu skalieren (also seine Grösse zu verändern) müssen wir lediglich jeden Scheitelpunkt eines Objektes mit einem Skalierungs_Faktor multiplizieren:

X_Neu = Skalierungs_Faktor * X_Alt
y_Neu = Skalierungs_Faktor * Y_Alt
Z_Neu = Skalierungs_Faktor * Z_Alt

Es gilt dabei zu beachten, dass diese Operation die tatsächliche Grösse eines Objektes ändert. Die perspektivische Vergrösserung eines Objektes (das sich dem Betrachter zum Beispiel nähert) wird bereits durch die Projektion erledigt. Das Skalieren kann also zum Beispiel bei Morphing Effekten verwendet werden.
Wie bei der Verschiebung finden wir auch hier eine Matrix, mit der wir eine Skalierung mit drei verschiedenen Faktoren für einen Punkt durchführen können:

Rotation

Der schwierigste Teil der Transformationsoperationen sind die drei möglichen Rotationen um die drei Achsen unseres Cyberspace. Das erfordert ein wenig Mathematik doch diese wollen wir hier überspringen und gemäss unseres Mottos "Man muss nicht wissen wie es geht, man muss nur wissen wo es steht!" einfach nur das Endergebnis dieser Berechnungen angeben.
Wenn man ein Objekt um eine Achse rotieren will, so muss man einfach jeden Scheitelpunkt dieses Objektes mit den gleich folgenden Formeln modifizieren. Deshalb ist es auch wichtig, dass jedes Objekt unseres Cyberspace ein lokales Koordinatensystem besitzt. Der lokale Urpsrung eines Objektes ist dann nämlich der Punkt, um den ein Objekt rotiert wird. Lassen wir nun ein Raumschiff durch unser virtuelles Universum fliegen und rotieren es um die x-Achse, um einen Steigflug durchzuführen. Die folgende Bildsequenz zeigt an, wie unterschiedlich definierte Ursprünge im lokalen Koordinatensystem diese Rotation ausführen würden.

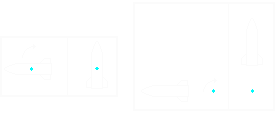
Deshalb ist es wichtig, dass jedes Objekt sein eigenes lokales Koordinatensystem besitz. In diesem wird dann die Rotation durchgeführt und erst dann werden die neu berechneten Koordinaten in Weltkoordinaten umgerechnet. Würde man die Weltkoordinaten rotieren, so würde das Objekt nicht nur rotiert, sondern auch verschoben (wie obige Grafik zeigt).

Doch wie sehen nun die Formeln für die Rotationen aus? In unserem dreidimensionalen Raum können wir ein Objekt um jede der drei Achsen rotieren. Dafür müssen wir die Koordinaten jedes Scheitelpunktes des betroffenen Objektes anhand mathematischer Formeln neu berechnen. Bei der jeweiligen Rotation bleibt immer diejenige Koordinate unverändert, um deren Achse wir rotieren. Hier nun also endlich die Formeln:

Rotation um die z-Achse:
x' = x * cos(Rotation_z) - y * sin(Rotation_z)
y' = x * sin(Rotation_z) + y * cos(Rotation_z)

Rotation um die x-Achse:
y' = y * cos(Rotation_x) - z * sin(Rotation_x)
z' = y * sin(Rotation_x) + z * cos(Rotation_x)

Rotation um die y-Achse:
z' = z * cos(Rotation_y) - x * sin(Rotation_y)
x' = z * sin(Rotation_y) + x * cos(Rotation_y)

Wie auch schon bei der Verschiebung und der Skalierung finden wir wieder geeignete Matrizen die diese Aufgabe erfüllen. Diese lassen uns die Berechnungen übersichtlicher durchführen:
 

Rotation um die z-Achse:
Rotation um die x-Achse:
Rotation um die y-Achse:

Nun werden wir eine Methode basteln, mit der wir eine Rotation um drei Achsen ausführen können. Um das kleine Demoprogramm nicht zu sehr aufzublähen werden die Transformationen nicht alle implementiert. Hier werden allerdings die einfachen übersprungen, nämlich Verschiebung und Skalierung und "nur" die Rotationen aller drei Achsen implementiert. Dies ist mit Abstand die aufwendigste Transformation und die anderen beiden lassen sich ganz analog und wesentlich kürzer implementieren.
Die Rotationen werden nicht an konkreten Objekten wie unseren Rectangle3D oder Point3D Klassen durchgeführt, sondern speichern die Ergebnisse der Drehwinkel in der Haupttransformationsmatrix.

// Haupttransformationsmatrix
double mm[][] = new mm[4][4];

public void rotate(double ax, double ay, double az) {
  // x-Rotationsmatrix
  if (ax!=0.0) {
      double mat1[][] = new double[4][4];
      double xmat[][] = new double[4][4];

      xmat[0][0]=1; xmat[0][1]=0;
      xmat[0][2]=0; xmat[0][3]=0;
 

Da ein Würfel sechs Seiten hat, übergeben wir dem Konstruktor einfach sechs Rectangle3D Objekte und speichern diese in einem Array ab. Nun müssen wir unser obiges Programm einfach so erweitern, dass alle Methoden, die ein Rectangle3D Objekt bearbeiten (z.B. project3DTo2D, backfaceCulling,...) in einer Schleife für alle sechs Flächen unseres Würfels aufgerufen werden - fertig! Damit unser Würfel auch etwas besser aussieht, erhält jedes Rectangle3D Objekt eine andere Farbe, womit auch die Verwendung der letzten unbekannten Variable dieser Klasse geklärt wäre.
Die Rotation muss übrigens trotzdem nur einmal ausgeführt werden, da sie ihre Ergebnisse ja in der Hauptransformationsmatrix abspeichert. Durch den Aufruf der createWorldCoordinates Methode für alle sechs Flächen transformieren wir alle diese Flächen mit der Haupttransformationsmatrix und sparen so viel Rechenarbeit, indem wir die Rotationsmatrizen nicht für alle sechs Objekte neu berechnen, das ist der Vorteil der Verwendung von Matrizen bei 3D Engines!
 

4.Die Augen des Betrachters

Nun kommen wir zu dem letzten grossen Schritt, um unseren Cyberspace aus dem Computerspeicher heraus auf den Bildschirm zu katapultieren. Unser Cyberspace enthält nun dreidimensionale Objekte die wir skalieren, anordnen und rotieren können, doch existiert unser virtuelles Universum nur im RAM des Computers und wir haben noch keine Möglichkeit, es sichtbar zu machen (ausser in Zahlenkolonnen und mathematischen Formeln, was aber nicht sehr aufregend wäre).
Wir haben zwar schon die Projektion angesprochen, mit der man Koordinaten von 2D in 3D Räume projizieren kann, uns fehlen aber noch ein paar Details. Dieser Abschnitt beschäftigt sich mit der Bewegung des Betrachters und dem sogenannten Clipping.

Bewegung des Betrachters

Uns stehen zwar Mittel zur Verfügung, Objekte unseres Cyberspace zu bewegen, wie aber ist es mit dem Betrachter selbst? Die bisherige Darstellung geht davon aus, dass der Betrachter sich am Ursprung des Weltkoordinatensystems befindet und dort verbleibt. Das allein wäre aber ziemlich langweilig, doch können wir den Betrachter nicht wie die Objekte unserer Welt bewegen und rotieren, schliesslich besteht er nur aus einem Satz von Koordinaten und Rotationswinkeln.
Wie bewegen wir den Betrachter also? Es ist tatsächlich so einfach, denn für die visuelle Wahrnehmung eines Menschen macht es keinerlei Unterschied, ob er sich zu einem Objekt hinbewegt oder ob das Objekt sich zu ihm bewegt - vorausgesetzt das Objekt ist der einzige Bezugspunkt des Menschen. Da unser virtuelles Universum später viele Bezugspunkte haben wird, umgehen wir das Problem indem wir einfach alle Bezugspunkte ebenfalls entsprechend bewegen.
Lange Rede, kurzer Sinn:
Wenn unser Betrachter einen Schritt vorwärts tun will implementieren wir das, indem wir alle Objekte einen Schritt in entgegengesetzter Richtung ausführen lassen. Und wenn der Betrachter 90 Grad nach rechts schauen will, dann rotieren wir einfach alle Objekte um 90 Grad nach links.
Warum funktioniert das? Weil wir die Weltkoordinaten der Objekte modifizieren! Wenn wir uns noch mal den Abschnitt über Rotation ins Gedächnis rufen, so werden wir uns erinnern, dass wir ein Objekt um seinen lokalen Ursprung rotiert haben, weil wir sonst eine Verschiebung erzeugt hätten. Doch genau diese Verschiebung wollen wir ja jetzt erreichen. Wenn der Betrachter nach rechts blickt, so dreht sich nicht nur der Betrachtungswinkel zu dem Objekt, sondern das Objekt bewegt sich scheinbar auch nach links.

Wenn wir nun voraussetzen, dass wir bereits die Funktionen zur Verschiebung und Rotation implementiert haben, bewegen wir also unseren Betrachter wie oben beschrieben durch folgenden Algorithmus:

for (alle Objekte)
   {
   Verschiebe_Objekt(Objekt, -Betrachter.pos_x, -Betrachter.pos_y, -Betrachter_pos_z);
   Rotiere_Objekt(Objekt, -Betrachter.winkel_x, -Betrachter.winkel_y, -Betrachter.winkel_z);
   }

 

Clipping

Um nun den finalen Schritt der Bildschirmausgabe vollziehen zu können, müssen wir unser komplettes mathematisches Universum derart beschneiden, dass nur der Teil davon zur Ausgabe kommt, der wirklich im sichtbaren Bereich liegt. Das erledigen wir durch das Clipping. Zum einen durch das Objekt-Clipping zum anderen durch das Image-Clipping.

Dafür müssen wir aber erstmal etwas genauer auf unsere Objekte eingehen. Wir werden ab hier voraussetzen, dass wir unsere Objekte so implementiert haben, dass wir das Objekt in einer Struktur gespeichert haben, die unter anderem ein Feld mit allen Polygonen(Seitenflächen) enthält.

Objekt-Clipping:
Nachdem nun alle Objekte transformiert und an den Blickpunkt des Betrachters angepasst sind, überprüfen wir nun die Sichtbarkeit der Objekte für den Betrachter. Das folgende Bild zeigt, dass das Blickfeld des Betrachters ein Pyramidenstumpf mit sechs Seiten darstellt.

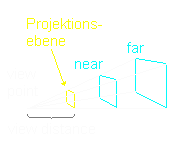
Die blau markierten Flächen bezeichnen die near und far Clipping-Planes für die z-Achse. Objekte die hinter dem far Plane liegen sind zu weit entfernt, um vom Betrachter gesehen zu werden. Ein Mensch kann zwar theoretisch unendlich weit sehen, ab einer gewissen Entfernung sind die Objekte jedoch zu klein, um wahrgenommen zu werden. Der Computer würde diese aber hartnäckig weiterhin zeichnen, egal wie klein sie sind, und wertvolle Rechnerzeit darauf verschwenden. Objekte die vor dem near Plane liegen, sind hinter dem Betrachter, bzw. viel zu nah um gezeichnet zu werden.
Der erste Test des Objekt-Clipping überprüft nun, ob die Weltposition eines Objektes überhaupt innerhalb dieser beiden Flächen liegt. Wenn nicht, dann braucht das Objekt überhaupt nicht gezeichnet zu werden, da es zu weit weg ist oder hinter dem Betrachter.
Für alle Objekte innerhalb dieser Grenzen wiederholt man diesen Test für alle Polygone des Objektes. Dabei testet man analog ob ALLE Eckpunkte eines Polygons ausserhalb des Bereichs liegen und setzt dann für dieses Polygon ein entsprechendes Flag auf TRUE.
Das hat den Sinn, dass die 3D Engine das eigentliche Zeichnen der Objekte übernimmt und zwar zeichnet man ein Objekt, indem man seine Polygone zeichnet. Wir sparen nun ganz erheblich Rechenzeit ein, wenn wir an unsere Zeichenfunktion nur solche Objekte weitergeben, deren Clip Flag auf FALSE steht und innerhalb dieser Funktion wiederum nur alle Polygone an Glide zum zeichnen übergeben, deren Clip Flag ebenfalls auf FALSE steht.

Image-Clipping:
Nun haben wir bereits alle Objekte und Polygone aussortiert, die komplett ausserhalb des sichtbaren Bereichs auf der z-Achse liegen. Was ist nun aber mit den vier anderen Seiten unseres Pyramidenstumpfes?
Dieses Problem gehen wir an, indem wir die Weltkoordinaten projizieren und damit die zweidimensionalen Bildschirmkoordinaten x und y aller Punkte des Objektes erhalten.
Anhand dieser Bildschirmkoordinaten testen wir nun alle Polygone, die bisher noch das Clip FlagFALSEClip Flag auf TRUE.

Nun haben wir bereits alle Objekte aussortiert, die vollständig nicht sichtbar sind. Ebenso die vollständig nicht sichtbaren Polygone derjenigen Objekte die zum Teil sichtbar sind. Was uns nun noch fehlt ist eine Methode um zu überprüfen, ob ein Polygon zum Teil sichtbar ist. Bisher haben wir immer nur ganze Objekte oder wenigstens ganze Polygone entfernt, doch was machen wir, wenn ein Polygon nicht vollständig auf dem Bildschirm ist, aber wenigstens zum Teil?
Die Antwort ist wiederum relativ einfach: Wir überprüfen JEDEN der letztendlich zu zeichnenen Punkte der gesamten Polygonfläche ob er innerhalb der zulässigen x- und y-Grenze des Bildschirms liegt.
 
 

Zusammenfassung

Nun noch ein Wort zu den Transformationsoperationen. Kurz und knapp gesagt kann man alle Transformationen anwenden, indem man die Skalierungs-, die Verschiebungs- und die drei Rotationsmatrizen erzeugt, miteinander multipliziert und dann alle Punkte des Objektes mit dieser Gesamtmatrix multipliziert. Dabei kommt man allerdings in die Lage, eventuell viele unnötige Berechnungen anzustellen. Besser ist es, Verschiebung und Skalierung ohne Matrizen direkt auf die Koordinaten anzuwenden und bei Rotationen alle möglichen Kombinationen der drei Rotationsachsen vorherzuberechnen und daraus alle möglichen Gesamtmatrizen vorherzuberechnen, um die Koordinaten zu modifizieren.
Ebenso bekommt man schnelleren Code, wenn man die Matrizenoperationen ohne Schleifen programmiert und anstelle dessen quasi "von Hand" die notwendigen Formeln für alle 3 zu berechnenden Koordinaten benutzt.

Nun haben wir bereits fast alle Schritte kennengelernt die nötig sind, um eine 3D Engine zu implementieren. Bisher sind wir aber immer nur auf die einzelnen Schritte eingegangen, ohne den globalen Zusammenhang herzustellen. Nun werden wir ein grobes Schema aufstellen, wie eine 3D Engine vom Ablauf her aussehen sollte.

Eine 3D Engine wird also die folgenden Schritte in gegebener Reihenfolge vornehmen:

  Schritt 1:
  - Lade alle Objekte

  Schritt 2:
  - USERCODE (Eingaben für Bewegungen der Objekte usw.)

  Schritt 3:
   - Skaliere und rotiere die lokalen Koordinaten aller Objekte
   - Verschiebe die Weltposition aller Objekte
   - Verschiebe und rotiere den Betrachter

  Schritt 4:
  - Erzeuge die Weltkoordinaten aller Objekte
 - Erzeuge die inverse Kameramatrix

  Schritt 5:
  - Verschiebe und rotiere alle Objekte mit der inversen Kameramatrix

  Schritt 6:
  - USERCODE (Kollisionsabfragen usw.)

  Schritt 7:
  - Zeichne alle sichtbaren Objekte

Vielleicht sollte man die Begriffe Weltposition und Weltkoordinaten der Objekte nochmal erläutern. Die Weltposition legt die Position des lokalen Urpsprungs des Objektes in unserem Cyberspace fest. Die Weltkoordinaten des Objektes werden dann berechnet, indem man alle (transformierten) lokalen Koordinaten des Objektes mit den Weltkoordinaten addiert.

Dieses allgemeine Ablaufschema sollte eigentlich gut verdeutlichen, wie eine 3D Engine funktioniert. Selbst wenn man nicht das Wie-kommt-man-darauf hinter all den Schritten verstanden hat, so reicht es doch zu wissen, warum man das tun muss und wie man es mit Formeln berechnet. Nun sollte es kein Problem mehr sein, eine 3D Engine zu programmieren und unter uns gesagt, die meiste Arbeit der Engine erledigen heutzutage diverse API's wie beispielsweise Direct3D, Glide (Voodoo) oder Java3D...